📄 Project Page • Last updated:

DAPG: Distance-Aware Pruned Graph for Fast & Accurate ANN

A single-layer, geometry-aware pruning framework that builds compact, high-recall proximity graphs without hierarchical routing.

Solmaz Seyed Monir · Dr. Dongfang Zhao . ( University of Washington, University of Washington )
Paper (arXiv) Code (GitHub) BibTeX Results FAQ
DAPG teaser: geometry-aware pruning and query flow

Figure: The DAPG index structure for object set O. DAPG maintains a single adaptive layer where each node oi keeps only nearby edges under its local percentile threshold Ï„oi. This provides a sparse but path-connected graph supporting dynamic insertion and deletion.

Abstract

DAPG introduces percentile-based local filtering and adaptive global sparsification to build degree-adaptive proximity graphs that preserve reachability while reducing redundant edges. DAPG improves latency–recall trade-offs over state-of-the-art (SOTA) baselines without multi-layer indexing.

+3.3% recall 2.9× faster Single layer LSH seeding compatible

Summary

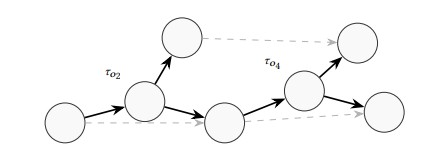
Fixed-degree pruning assumes uniform neighborhood sizes, disregarding spatial density variations and causing suboptimal graph connectivity. DAPG introduces a percentile-based local filtering mechanism that dynamically determines edge retention per node and an adaptive global sparsification policy that caps high-degree outliers. These mechanisms produce degree-stable, path-connected proximity graphs that preserve navigability while reducing redundant edges, resulting in lower traversal cost and improved recall–latency efficiency.

Highlights

  • Local percentile threshold τv + adaptive cap T'.
  • Cost model: CQ = O(¯dDAPG Î²(â„“)).
  • LSH seeding; no hierarchy.
  • Supports dynamic insertion and deletion with degree-stable connectivity.

Build

cd cppCode/DAPG
make

Run

./dapg sift   # expects dataset/sift.data_new

Method Overview

Local percentile thresholds adapt to density; global caps bound branching; LSH seeds initialize search.

Cost Model

Expected query cost factorizes into average degree and expansion depth.

C_Q = O(¯d_DAPG · β(â„“))
T_Q = O(d · ¯d_DAPG · β(â„“))
β(ℓ) = O(log n) under small-world routing

FAQ

Does DAPG require a hierarchy? single layer with geometry-aware pruning.

Can I swap the LSH backend? β(ℓ) is backend-dependent

Contact

Open an issue or email solmazsm@uw.edu.

© 2026 DAPG Authors.